Overview
This is a C++ console application built with Visual Studio to perform long division. The idea is to perform division without using the division operator. This was one of the first programs I wrote for myself. I wrote it during or after my first programming course in university which used C++. After doing all the exercises for the course I wanted to come up with something on my own and for some reason I was thinking about long division at the time so that’s what I did.
I enjoy long division. It’s very satisfying. With addition, subtraction or multiplication you just kind of go from right to left performing the operation for each part. With division you have to calculate the times table for your denominator and then iteratively test those values against the number you are trying to divide.
Interface
 Input
Input
The program starts by asking the user for two numbers, A and B. A is the numerator or the number being divided. B is the denominator or the number used to divide. Both must be whole numbers between 0 and 100,000,000.
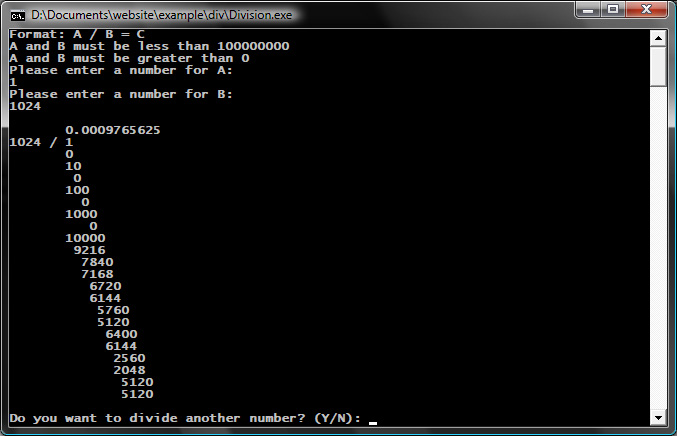 Output
Output
The program then performs the division and outputs the results in the format of long division. The top line is the result as a decimal value. The second line shows the operation being performed as you would write it out when doing long division with the slash standing in for the box around the numerator. Below that are the steps used to calculate the result.
 Repeat
Repeat
The program then asks the user if they want to perform another division. Choosing yes causes the program to reset and ask for the numbers again. Choosing no causes it to quit.
Code
div.cpp
The program starts by outputting the instructions. Next it reads the A and B values using two input loops. The loops start by printing a prompt. Next they read a value from the console and then try to convert that to a number. If it’s not a valid number or outside of the specified range it displays an invalid input error and loops again.
Next the program calculates the number of digits in each number and initializes the three arrays that it uses to keep track of information so that it can be displayed later. The output array stores the digits of the result. The curList array stores the remainder after each digit of the result is calculated. The mulList array stores the result digit multiplied by B which is what gets subtracted from the current remaining value to calculate the next remainder.
Next we loop through all the digits in A and calculate the result of A / B. We do this by seeing how many times B fits into the remainder we are currently working with. The first time through the loop this will just be the first digit from A but subsequent times it’ll be the next digit of A plus the previous remainder multiplied by 10. We loop through the values 0 to 9, add 1 to that value, multiply it by B and see if it’s greater than the current remainder. If it is then we know that the current loop value is the max number of times B fits into the current remainder. If the value is 0 and we haven’t found a non-zero value yet then we just iterate again. We use the NOPRINT constant to indicate that no value should be output for this value. If the value is our first non-zero result we put one more NOPRINT constant in curList. This is because we use A as the first line in the output. Otherwise we store the current remainder in curList so that it can be printed later. We store the loop value in the output array as it’s the next digit of the result and then we store that value multiplied by B in mulList so that it can be printed later. We then take the multiplied value and subtract it from the current remainder to get the remainder for the next iteration of the loop.
After completing the first loop we have calculated how many Bs fit entirely in A. If we still haven’t found a non-zero value then we put a 0 in output and mulList. Next we put the DECPRINT constant in each of the arrays to indicate where the decimal point should go.
We then calculate the fractional part of the result. The process is very similar to the whole number part except we aren’t getting more digits from A or worried about non-zero values. We simply find the smallest value multiplied by B that fits in our current remainder and update or three arrays. After each iteration we check if the remainder is 0 and break out of the loop if it is, otherwise we loop until we’ve reached the MAXDEC constant.
At this point we’ve calculated the entire result or at least we’ve calculated it up to a certain number of digits. We start printing the result by writing spaces to the console. The number of spaces is based on the number of digits in B plus 3. Next we print the result by looping through the values in the output array. NPRINT values are replaced with spaces and DECPRINT is replaced by a ‘.’. On the next line we print “<B> / <A>”. The “ / “ separator is where the plus 3 comes from in calculating the number of spaces before the result.
Finally we get to printing the intermediate steps. We loop through all the possible digits in the result. If the value in mulList is NOPRINT we simply move to the next iteration. If the value is DECPRINT then we correct our spacing calculation so things continue to line up and move to the next iteration. If the curList value for the current digit isn’t NOPRINT we print it on the next line. We calculate the spacing in front of the value by adding up the number of digits in B, the number of times we’ve gone through the loop, our base spacing value and the number of digits in the current remainder. The base spacing value starts as 4 and then gets change to 3 after the decimal point has been reached. On the next line we print out the multiplied value stored in mulList using similar spacing logic.
For example if you look at the second screenshot above you can see there are 7 spaces before the result. That’s 4 digits from the size of B plus 3 from the separator. The first mulList value also has 7 spaces. Because this is the first digit we know the loop index is 0 so we add that to the number of digits in B (4) and the spacing value (4) and then subtract the number of digits in the multiplied value (1) to get 7 (0 + 4 + 4 – 1). On the next iteration we get the decimal point so we won’t print anything but the spacing value will be changed to 3. Next we print out the first curList value. This time the loop index is 2, the spacing value is 3, the size of B is 4 and the size of the value is 2 which gives us 7 (2 + 3 + 4 – 2) so that the value lines up with the previous value.
After printing the result we ask the user if they want to divide some different numbers. We then read a line of input from the user. If the line starts with a upper or lowercase y we loop and start again, otherwise we break out of the loop and the program exits.
The getDigits(int number) function returns a count of the digits, in base 10, in number. This is calculated by repeatedly multiplying number by 0.1, effectively dividing by 10, casting the result to an integer to remove the fractional part and checking if number is 0. How many times number had to be multiplied by 0.1 before the result is 0 is how many digits there are in number.
The getNextDigit(int &number) function removes the left most digit from number and returns it. The function first gets a count of the digits in number. It uses a loop to calculate the base value of the last digit in number and the inverse of that value. The base value being the number you would have to multiply a digit by in order to get it into that value. For example in the number 342 the left most digit is 3 and the base power of that digit is 100. The number is multiplied by the inverse base power to make it so that the left most digit is the only one on the left side of the decimal place. The result is cast to an integer to remove the other digits. The left most digit is then multiplied by the base power and then subtracted from number. This removes the left most digit from number. The left most digit is then returned by the function. (Note: a power function isn’t used here either because I didn’t know of one or because I wanted to make sure it wasn’t sneakily using division to calculate a negative power)